10203. Арктическая сеть

Министерство национальной обороны (МНО) планирует соединить несколько северных форпостов в единую беспроводную сеть. Для построения сети должны использоваться две различные технологии связи: каждая застава будет оснащена радиоприёмником, а некоторые из них дополнительно получат спутниковый канал.

Любые два аванпоста, имеющие спутниковый канал, могут связываться между собой через спутник, независимо от расстояния между ними. В противном случае два аванпоста могут обмениваться данными по радио только в том случае, если расстояние между ними не превышает d, зависящее от мощности трансиверов. Чем выше мощность, тем больше значение d, однако стоимость оборудования при этом также возрастает. По экономическим и эксплуатационным соображениям все трансиверы должны быть одинаковыми, то есть значение d должно быть одинаковым для всех пар форпостов.

Определите минимальное значение d, при котором обеспечивается связь между любыми двумя аванпостами – напрямую или через другие заставы (по цепочке соединений).

Вход. Первая строка содержит количество тестов n. В первой строке каждого теста указаны количество спутниковых каналов s (1 ≤ s ≤ 100) и количество аванпостов p (s < p ≤ 500). Далее следуют p строк, каждая из которых содержит координаты (x, y) соответствующей заставы в километрах (целые числа от 0 до 10000).

Выход. Для каждого теста выведите минимальное значение d, необходимое для соединения всех аванпостов в сеть. Результат следует вывести с точностью до двух десятичных знаков.

Пример входа	Пример выхода
1 2 4 1 0 3 0 6 0 7 2	2.24

РЕШЕНИЕ

графы – алгоритм Прима

Анализ алгоритма

Запустим алгоритм Прима. Построим массив dist, в котором dist[i] хранит длину кратчайшего ребра из минимального остова, входящего в вершину i. То есть как раз из этих ребер и состоит минимальный остов. При этом dist[0] = 0, так как стартуем алгоритм из вершины 0.

По окончанию алгоритма Прима отсортируем массив dist. Спутниковыми каналами следует соединить наиболее отдаленные аванпосты. Их следует разместить в тех s аванпостах, которые соединяют самые длинные ребра из dist (s – 1 ребро соединяет s аванпостов). Следовательно искомым значением d будет длина ребра, являющегося s-ым с конца dist.

Пример

Рассмотрим пример, приведенный в условии.

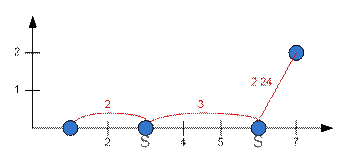
Два спутниковых канала ставим в точках (3; 0) и (6; 0). Таким образом заставы в этих координатах связываются через спутник. Среди оставшихся ребер минимального остовного дерева ищем наибольшее. Таким будет ребро, соединяющее точки (6; 0) и (7; 2), его длина равна 2.24.

Реализация алгоритма

Объявим глобальные массивы. Координаты застав храним в (x[i], y[i]). Значение used[i] = 1, если вершина i включена в остов.

#define MAX 501

#define INF 0x3F3F3F3F

int x[MAX], y[MAX];

int used[MAX], dist[MAX];

Функция dist2 вычисляет квадрат расстояния между заставами i и j.

int dist2(int i, int j)

{

return (x[j] - x[i])*(x[j] - x[i]) + (y[j] - y[i])*(y[j] - y[i]);

}

Функция Prim реализует алгоритм Прима.

void Prim(void)

{

Инициализируем массивы.

memset(dist, 0x3F, sizeof(dist));

memset(used, 0, sizeof(used));

Начинаем строить минимальный остов с вершины 0. Инициализируем dist[0] = 0, used[0] = 1.

int i, j, cur = 0;

dist[cur] = 0;

used[cur] = 1;

Совершаем n – 1 итерацию. На каждой итерации в остов добавляем одну вершину (так что в остов еще следует добавить n – 1 вершин).

for (i = 1; i < n; i++)

{

Текущей вершиной является cur. Перебираем ребра (cur, j) и пересчитываем значение dist[j]. Таким образом dist[j] хранит текущее кратчайшее расстояние от вершины j до текущего минимального остова.

for (j = 0; j < n; j++)

if (!used[j] && (dist2(cur, j) < dist[j]))

dist[j] = dist2(cur, j);

Ищем ребро наименьшей длины, которое будет включено в остов. Для этого ищем такое наименьшее dist[j], что вершина j еще не принадлежит остову (used[j] = 0). Номер вершины с наименьшим dist[j] заносим в cur (она становится текущей).

int min = INF;

for (j = 0; j < n; j++)

if (!used[j] && (dist[j] < min))

{

min = dist[j];

cur = j;

}

Вершина cur включается в остов.

used[cur] = 1;

}

}

Основная часть программы. Обрабатываем tests тестов.

scanf("%d", &tests);

while (tests--)

{

Читаем входные данные.

scanf("%d %d", &s, &n);

for (i = 0; i < n; i++)

scanf("%d %d", &x[i], &y[i]);

Запускаем алгоритм Прима.

Prim();

Сортируем массив dist.

sort(dist, dist + n);

Выводим ответ.

printf("%.2lf\n", sqrt(dist[n - s]));

}

Java реализация

import java.util.*;

public class Main

{

static int n;

static int x[], y[];

static int used[], dist[];

static int dist2(int i, int j)

{

return (x[j] - x[i])*(x[j] - x[i]) + (y[j] - y[i])*(y[j] - y[i]);

}

static void Prim()

{

dist = new int[n];

Arrays.fill(dist, Integer.MAX_VALUE);

used = new int[n];

int i, j, cur = 0;

dist[cur] = 0;

used[cur] = 1;

for (i = 1; i < n; i++)

{

for (j = 0; j < n; j++)

if (used[j] == 0 && dist2(cur, j) < dist[j])

dist[j] = dist2(cur, j);

int min = Integer.MAX_VALUE;

for (j = 0; j < n; j++)

if (used[j] == 0 && dist[j] < min)

{

min = dist[j];

cur = j;

}

used[cur] = 1;

}

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int tests = con.nextInt();

while (tests-- > 0)

{

int s = con.nextInt();

n = con.nextInt();

x = new int[n];

y = new int[n];

for (int i = 0; i < n; i++)

{

x[i] = con.nextInt();

y[i] = con.nextInt();

}

Prim();

Arrays.sort(dist);

System.out.println(Math.sqrt(dist[n - s]));

}

con.close();

}

}